how do you draw a pyramid in 3d

• Download source files - 23.seven KB

Introduction

Commonly, the Cartesian coordinate system is used in transformations and projections for graphics objects. In this case, you but specify a point using Ten, Y, and Z coordinates. In practice, other coordinate systems tin also be applied, and are sometimes more convenient than the Cartesian coordinate system.

In this article, I will discuss the spherical coordinate system in 3D space and show you how to create the spherical graphics objects in this organization.

Background

In the spherical coordinate organisation, a point is specified by r, θ, and φ. Here r is the distance from the bespeak to the origin, θ is the polar bending, and φ is the azimuthal angle in the X-Z plane from the X centrality. In this notation, I alternate the conventional Y and Z axes so that the computer screen is described by the Ten-Y plane. Figure one shows a signal in this spherical coordinate system

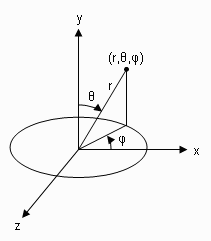
Figure ane: Spherical coordinate system.

From this figure, nosotros can obtain the post-obit relationships:

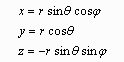
The spherical coordinates (r, θ, φ) are related to the Cartesian coordinates by:

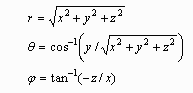
Sometimes it is more than user-friendly to create sphere-like objects in terms of the spherical coordinate organization. The following example awarding programme volition create ii spheres. We need to add the Matrix3 and Point3 classes to the current projection. And likewise add together a new form, DrawSphere, to the project.

Now we need to add together a Spherical method to the Matrix3 class. The Matrix3 grade has been discussed in Chapter 5 of my new book "Practical C# Charts and Graphics".

          public          Point3 Spherical(float          r,          float          theta,          float          phi)  {     Point3 pt =          new          Point3();          float          snt = (float)Math.Sin(theta * Math.PI /          180);          float          cnt = (float)Math.Cos(theta * Math.PI /          180);          float          snp = (float)Math.Sin(phi * Math.PI /          180);          float          cnp = (bladder)Math.Cos(phi * Math.PI /          180);      pt.X = r * snt * cnp;      pt.Y = r * cnt;      pt.Z = -r * snt * snp;      pt.W =          1;          return          pt;  }        

This method transforms a point in the spherical coordinate arrangement to a point in the Cartesian coordinate system. We then Add together a DrawSphere class to the projection. This class allows you to specify the radius and positions (the center location) of a sphere object. The SphereCoordinates method in this class creates the points on a sphere surface by specifying their longitude and latitude. The DrawIsometricView draws the sphere using the isometric projection.

Using the code

This application can be tested using the post-obit Form1 class:

          using          System;          using          Organisation.Cartoon;          using          System.Drawing.Drawing2D;          using          System.Windows.Forms;          namespace          Example5_6  {          public          partial          course          Form1 : Form     {          public          Form1()        {              InitializeComponent();          this.SetStyle(ControlStyles.ResizeRedraw,          true);                           panel1.Paint +=          new          PaintEventHandler(panel1Paint);        }          individual          void          panel1Paint(object          sender, PaintEventArgs eastward)        {              Graphics chiliad = e.Graphics;              k.SmoothingMode = SmoothingMode.AntiAlias;          float          a = panel1.Top /          iii;              DrawSphere ds =          new          DrawSphere(this, a,          0,          0, -a /          2);              ds.DrawIsometricView(m);              ds =          new          DrawSphere(this,          2          * a /          3, -a/2, -a/two, a /          2);              ds.DrawIsometricView(grand);        }      }  }        

Hither we create two spheres with unlike radii and positions. Past building and running this project, you should obtain the results shown in Figure two.

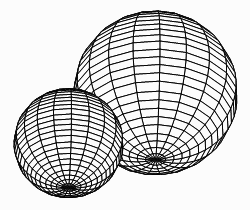
Figure 2: Spheres created in a spherical coordinate system.

This project is from the examples (example5-vi in Chapter five) of the new book "Practical C# Charts and Graphics", where you tin find more advanced chart and graphics programming for real-globe .NET applications. For more data, please visit the website at world wide web.publishing.unicadinc.com

About the Author

Dr. Jack Xu has a Ph.D in theoretical physics. He has over 15 years programming experience in Basic, Fortran, C, C++, Matlab, and C#, specializing in numerical computation methods, algorithms, physical modeling, figurer-aided pattern (CAD) development, graphics user interface, and 3D graphics. Currently, he is responsible for developing commercial CAD tools based on Microsoft .Net framework.

Please read my other articles:

• "Draw Us Flag using C# and GDI+"
• "Create Custom Color Maps in C#"
• "Create a Custom Color Shading in C#"

mckinneyhispeauncer.blogspot.com

Source: https://www.codeproject.com/Articles/18160/Spherical-Coordinates-in-C